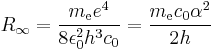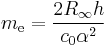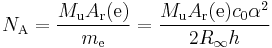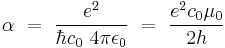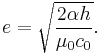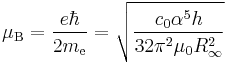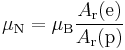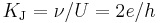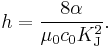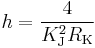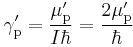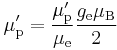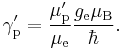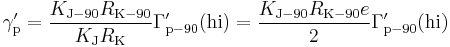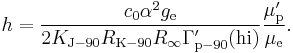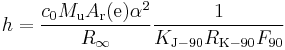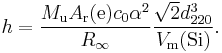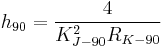Planck constant
| Values of h | Units |
|---|---|
| 6.62606896(33)×10−34 | J·s |
| 4.13566733(10)×10−15 | eV·s |
| 6.62606896(33)×10−27 | erg·s |
| Values of ħ | Units |
| 1.054571628(53)×10−34 | J·s |
| 6.58211899(16)×10−16 | eV·s |
| 1.054571628(53)×10−27 | erg·s |

The Planck constant (denoted h), also called Planck's constant, is a physical constant reflecting the sizes of quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory. The Planck constant was first described as the proportionality constant between the energy (E) of a photon and the frequency of its associated electromagnetic wave (ν). This relation between the energy and frequency is called the Planck relation or the Planck–Einstein equation:
Since the frequency ν, wavelength λ, and speed of light c are related by λν = c, the Planck relation can also be expressed as
Louis de Broglie generalized this, postulating that the Planck constant represents the proportionality between the energy and the quantum wavelength of not just the photon, but any particle.
A closely related constant is the reduced Planck constant, sometimes called the Dirac constant. It is equal to the Planck constant divided by (or reduced by) 2π, and denoted ħ ("h-bar"):
The reduced Planck constant is used when frequency is expressed in terms of radians per second ("angular frequency") instead of cycles per second. The energy of a photon with angular frequency ω is given by
Planck conjectured correctly that under certain conditions, energy could not take on any indiscriminate value. Instead, the energy must be some multiple of a very small quantity (later to be named a "quantum"). This is counterintuitive in the everyday world, where it is possible to "make things a little bit hotter" or "move things a little bit faster", This is because the quanta of energy are very, very small in comparison to everyday human experience. Thus, on the macro scale quantum mechanics and classical physics converge. Nevertheless, it is impossible, as Planck found out, to explain some phenomena without accepting that energy is quantized; that is, it exists only in integer multiples of some base value.
Contents |
Value
The Planck constant has dimensions of energy multiplied by time, which are also the dimensions of action. In SI units, the Planck constant is expressed in joule seconds (J·s). The dimensions may also be written as momentum multiplied by distance (N·m·s), which are also the dimensions of angular momentum.
The value of the Planck constant is:[1]
The value of the reduced Planck constant is:
The two digits between the parentheses denote the standard uncertainty in the last two digits of the value. The figures cited here are the 2006 CODATA recommended values for the constants and their uncertainties. The 2006 CODATA results were made available in March 2007 and represent the best-known, internationally-accepted values for these constants, based on all data available as of 31 December 2006. New CODATA figures are scheduled to be published approximately every four years.
Reduced Planck constant
As quantum mechanics was developed, it was found that very often when h appeared in equations, it was divided by  . The reduced Planck constant,
. The reduced Planck constant,
was introduced to simplify the notation.
The reduced Planck constant is used when frequency is expressed in terms of radians per second instead of cycles per second. The expression of a frequency in radians per second is often called angular frequency (ω), where ω = 2πν. The energy of a photon with angular frequency ω is given by
Significance of the size
The numerical value of the Planck constant depends entirely on the system of units used to measure it. When it is expressed in SI units, it is one of the smallest constants used in physics. In part, this reflects the fact that, on a scale where energies are measured in joules or kilojoules and times are measured in seconds or minutes, the effects of quantization are themselves very small. However, in part, it is also an artifact of the measuring system.
To take one example, green light of a wavelength of 555 nanometres (approximately the wavelength to which human eyes are most sensitive) has a frequency of 540 THz (540 × 1012 Hz). Each photon has an energy E of hν = 3.58 × 10−19 J. That is still a very small energy in terms of everyday experience, but then everyday experience doesn't deal with individual photons any more than it deals with individual atoms or molecules. To get a more macroscopic view, the energy of one mole of photons can be calculated by multiplying by the Avogadro constant, NA ≈ 6.022 × 1023 mol−1. Green light of wavelength 555 nm has an energy of 216 kJ/mol, equivalent to the strength of some types of chemical bond.
When the reduced Planck constant is treated as a conversion factor between phase, in radians, and action, in joule-seconds (as seen in the Schrödinger equation), it may be written with units J·s/rad.
The Planck constant is an atomic-scale constant and, even at the atomic scale, it has a small numerical value simply because frequencies tend to have large numerical values. The electronvolt is an atomic-scale unit of energy: each photon of green light has an energy of 2.23 eV. If time is measured in units which are much smaller than seconds, the numerical value of the Planck constant would become much larger. Atomic units are one such scale of measurement, in which the units of energy and time are chosen (indeed defined) so that the value of the reduced Planck constant is exactly one.
Origins
Black-body radiation
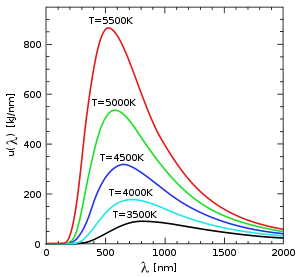
In the last years of the nineteenth century, Planck was investigating the problem of black-body radiation first posed by Kirchhoff some forty years earlier. It is well known that hot objects glow, and that hotter objects glow brighter than cooler ones. The reason is that the electromagnetic field obeys laws of motion just like a mass on a spring, and can come to thermal equilibrium with hot atoms. When a hot object is in equilibrium with light, the amount of light it absorbs is equal to the amount of light it emits. If the object is black, meaning it absorbs all the light that hits it, then it emits the maximum amount of thermal light too.
The assumption that blackbody radiation is thermal leads to an accurate prediction: the total amount of emitted energy goes up with the temperature according to a definite rule, the Stefan–Boltzmann law (1879–84). But it was also known that the colour of the light given off by a hot object changes with the temperature, so that "white hot" is hotter than "red hot". Nevertheless, Wilhelm Wien discovered the mathematical relationship between the peaks of the curves at different temperatures, by using the principle of adiabatic invariance. At each different temperature, the curve is moved over by Wien's displacement law (1893). Wien made a guess for the spectrum of the object, which was correct at low frequencies (long wavelength) but not at high frequencies (short wavelength). It still wasn't clear why the spectrum of a hot object had the form that it has (see diagram).
Planck hypothesized that the equations of motion for light are a set of harmonic oscillators, one for each possible frequency. He examined how the entropy of the oscillators varied with the temperature of the body, trying to match Wien's law, and was able to derive an approximate mathematical function for black-body spectrum.[2]
However, Planck soon realized that his solution was not unique. There were several different solutions, each of which gave a different value for the entropy of the oscillators,[2]. To save his theory, Planck had to resort to using the then controversial theory of statistical mechanics,[2] which he described as "an act of despair … I was ready to sacrifice any of my previous convictions about physics."[3] One of his new boundary conditions was
to interpret UN [the vibrational energy of N oscillators] not as a continuous, infinitely divisible quantity, but as a discrete quantity composed of an integral number of finite equal parts. Let us call each such part the energy element ε;—[2]
With this new condition, Planck had imposed the quantization of the energy of the oscillators, "a purely formal assumption … actually I did not think much about it…" in his own words,[4] but one which would revolutionize physics. Applying this new approach to Wien's displacement law showed that the "energy element" must be proportional to the frequency of the oscillator, the first version of what is now termed "Planck's relation":
Planck was able to calculate the value of h from experimental data on black-body radiation: his result, 6.55 × 10−34 J·s, is within 1.2% of the currently accepted value.[2] He was also able to make the first determination of the Boltzmann constant kB from the same data and theory.[5]
Prior to Planck's work, it had been assumed that the energy of a body could take on any value whatsoever – that it was a continuous variable. This is equivalent to saying that the energy element ε (the difference between allowed values of the energy) is zero, and therefore that h is zero. This is the origin of the often-quoted summary that "the Planck constant is zero in classical physics" or that "classical physics is quantum mechanics at the limit that the Planck constant tends to zero". The Planck constant, of course, is never zero, but it is so small compared to most human experience that its existence had been ignored prior to Planck's work.
The black-body problem was revisited in 1905, when Rayleigh and Jeans (on the one hand) and Einstein (on the other hand) independently proved that classical electromagnetism could never account for the observed spectrum. These proofs are commonly known as the "ultraviolet catastrophe", a name coined by Paul Ehrenfest in 1911. They contributed greatly (along with Einstein's work on the photoelectric effect) to convincing physicists that Planck's postulate of quantized energy levels was more than a mere mathematical formalism. The very first Solvay Conference in 1911 was devoted to "the theory of radiation and quanta".[6] Max Planck received the 1918 Nobel Prize in Physics "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta".
Photoelectric effect
The photoelectric effect is the emission of electrons (called "photoelectrons") from a surface when light is shined on it. It was first observed by Alexandre Edmond Becquerel in 1839, although credit is usually reserved for Heinrich Hertz,[7] who published the first thorough investigation in 1887. Another, particularly thorough investigation was published by Philipp Lenard in 1902.[8] Einstein's 1905 paper[9] discussing the effect in terms of light quanta would earn him the Nobel Prize in 1921,[7] when his predictions had been confirmed by the experimental work of Robert Andrews Millikan.[10] To put it another way, in 1921 at least, Einstein's theories on the photoelectric effect were considered more important than his theory of relativity (a name coined, as it happens, by Max Planck).[7]
Prior to Einstein's paper, electromagnetic radiation such as visible light was considered to behave as a wave: hence the use of the terms "frequency" and "wavelength" to characterise different types of radiation. The energy transferred by a wave in a given time is called its intensity. The light from a theatre spotlight is more intense than the light from a domestic lightbulb; that is to say that the spotlight gives out more energy per unit time (and hence consumes more electricity) than the ordinary bulb, even though the colour of the light might be very similar. Other waves, such as sound or the waves crashing against a seafront, also have their own intensity. However the energy account of the photoelectric effect didn't seem to agree with the wave description of light.
The "photoelectrons" emitted as a result of the photoelectric effect have a certain kinetic energy, which can be measured. This kinetic energy (for each photoelectron) is independent of the intensity of the light,[8] but depends linearly on the frequency;[10] and if the frequency is too low (corresponding to a kinetic energy for the photoelectrons of zero or less), no photoelectrons are emitted at all, however intense the light source.[10] Assuming the frequency is high enough to cause the photoelectric effect, a rise in intensity of the light source causes more photoelectrons to be emitted with the same kinetic energy, rather than the same number of photoelectrons to be emitted with higher kinetic energy.[8]
Einstein's explanation for these observations was that light itself is quantized; that the energy of light is not transferred continuously as in a classical wave, but only in small "packets" or quanta. The size of these "packets" of energy, which would later be named photons, was to be the same as Planck's "energy element", giving the modern version of Planck's relation:
Einstein's postulate was later proven experimentally: the constant of proportionality between the frequency of incident light (ν) and the kinetic energy of photoelectrons (E) was shown to be equal to the Planck constant (h).[10]
Atomic structure

Niels Bohr introduced the first quantized model of the atom in 1913, in an attempt to overcome a major shortcoming of Rutherford's classical model.[11] In classical electrodynamics, a charge moving in a circle should radiate electromagnetic radiation. If that charge were to be an electron orbiting a nucleus, the radiation would cause it to lose energy and spiral down into the nucleus. Bohr solved this paradox with explicit reference to Planck's work: an electron in a Bohr atom could only have certain defined energies En
where R∞ is an experimentally-determined constant (the Rydberg constant) and n is any integer (n = 1, 2, 3, …). Once the electron reached the lowest energy level (n = 1), it could not get any closer to the nucleus (lower energy). This approach also allowed Bohr to account for the Rydberg formula, an empirical description of the atomic spectrum of hydrogen, and to account for the value of the Rydberg constant R∞ in terms of other fundamental constants.
Bohr also introduced the quantity h/2π, now known as the reduced Planck constant, as the quantum of angular momentum. At first, Bohr thought that this was the angular momentum of each electron in an atom: this proved incorrect and, despite developments by Sommerfeld and others, an accurate description of the electron angular momentum proved beyond the Bohr model. The correct quantization rules for electrons – in which the energy reduces to the Bohr-model equation in the case of the hydrogen atom – were given by Heisenberg's matrix mechanics in 1925 and the Schrödinger wave equation in 1926: the reduced Planck constant remains the fundamental quantum of angular momentum. In modern terms, if J is the total angular momentum of a system with rotational invariance, and Jz the angular momentum measured along any given direction, these quantities can only take on the values
Uncertainty principle
The Planck constant also occurs in statements of Werner Heisenberg's uncertainty principle. Given a large number of particles prepared in the same state, the uncertainty in their position, Δx, and the uncertainty in their momentum (in the same direction), Δp, obey
where the uncertainty is given as the standard deviation of the measured value from its expected value. There are a number of other such pairs of physically measurable values which obey a similar rule. One example is time vs. frequency. The either-or nature of uncertainty forces measurement attempts to choose between trade offs, and given that they are quanta, the trade offs often take the form of either-or (as in Fourier analysis), rather than the compromises and grey areas of time series analysis. A practical example is computational neurology trying to both measure the time effect and frequency of a neuron burst. fMRI (functional MRI), whose signal processing is based on Fourier transforms, can resolve frequency, but not time (a limit of Fourier analysis due to uncertainty). An EEG (a time series analysis measurement tool) can resolve time, but not frequency. Due to uncertainty, these are not problems with the design of the measuring instruments, but problems with the nature of quantum measurement and particle realities themselves.
In addition to some assumptions underlying the interpretation of certain values in the quantum mechanical formulation, one of the fundamental corner-stones to the entire theory lies in the commutator relationship between the position operator  and the momentum operator
and the momentum operator  :
:
where δij is the Kronecker delta.
Notation
Unicode reserves codepoints U+210E (ℎ) for the Planck constant and U+210F (ℏ) for the reduced Planck constant.
Dependent physical constants
The following list is based on the 2006 CODATA evaluation;[1] for the constants listed below, more than 90% of the uncertainty is due to the uncertainty in the value of the Planck constant, as indicated by the square of the correlation coefficient (r2 > 0.9, r > 0.949). The Planck constant is (with one or two exceptions[12]) the fundamental physical constant which is known to the lowest level of precision, with a relative uncertainty ur of 5.0 × 10−8.
Rest mass of the electron
The normal textbook derivation of the Rydberg constant R∞ defines it in terms of the electron mass me and a variety of other physical constants.
However, the Rydberg constant can be determined very accurately (ur = 6.6 × 10−12) from the atomic spectrum of hydrogen, whereas there is no direct method to measure the mass of a stationary electron in SI units. Hence the equation for the calculation of me becomes
where c0 is the speed of light and α is the fine-structure constant. The speed of light has an exactly defined value in SI units, and the fine-structure constant can be determined more accurately (ur = 6.8 × 10−10) than the Planck constant: the uncertainty in the value of the electron rest mass is due entirely to the uncertainty in the value of the Planck constant (r2 > 0.999).
Avogadro constant
The Avogadro constant NA is determined as the ratio of the mass of one mole of electrons to the mass of a single electron: The mass of one mole of electrons is the "relative atomic mass" of an electron Ar(e), which can be measured in a Penning trap (ur = 4.2 × 10−10), multiplied by the molar mass constant Mu, which is defined as 0.001 kg/mol.
The dependence of the Avogadro constant on the Planck constant (r2 > 0.999) also holds for the physical constants which are related to amount of substance, such as the atomic mass constant. The uncertainty in the value of the Planck constant limits the knowledge of the masses of atoms and subatomic particles when expressed in SI units. It is possible to measure the masses more precisely in atomic mass units, but not to convert them more precisely into kilograms.
Elementary charge
Sommerfeld originally defined the fine-structure constant α as:
where e is the elementary charge, ε0 is the electric constant (also called the permittivity of free space), and μ0 is the magnetic constant (also called the permeability of free space). The latter two constants have fixed values in the International System of Units. However, α can also be determined experimentally, notably by measuring the electron spin g-factor ge, then comparing the result with the value predicted by quantum electrodynamics.
At present, the most precise value for the elementary charge is obtained by rearranging the definition of α to obtain the following definition of e in terms of α and h:
Bohr magneton and nuclear magneton
The Bohr magneton and the nuclear magneton are units which are used to describe the magnetic properties of the electron and atomic nuclei respectively. The Bohr magneton is the magnetic moment which would be expected for an electron if it behaved as a spinning charge according to classical electrodynamics. It is defined in terms of the reduced Planck constant, the elementary charge and the electron mass, all of which depend on the Planck constant: the final dependence on h½ (r2 > 0.995) can be found by expanding the variables.
The nuclear magneton has a similar definition, but corrected for the fact that the proton is much more massive than the electron. The ratio of the electron relative atomic mass to the proton relative atomic mass can be determined experimentally to a high level of precision (ur = 4.3 × 10−10).
Determination
| Method | Value of h (10−34 J·s) |
Relative uncertainty |
Ref. |
|---|---|---|---|
| Watt balance | 6.62606889(23) | 3.4 × 10−8 | [13][14][15] |
| X-ray crystal density | 6.6260745(19) | 2.9 × 10−7 | [16] |
| Josephson constant | 6.6260678(27) | 4.1 × 10−7 | [17][18] |
| Magnetic resonance | 6.6260724(57) | 8.6 × 10−7 | [19][20] |
| Faraday constant | 6.6260657(88) | 1.3 × 10−6 | [21] |
| CODATA 2006 recommended value |
6.62606896(33) | 5.0 × 10−8 | [1] |
| The nine recent determinations of the Planck constant cover five separate methods. Where there is more than one recent determination for a given method, the value of h given here is a weighted mean of the results, as calculated by CODATA. | |||
In principle, the Planck constant could be determined by examining the spectrum of a black-body radiator or the kinetic energy of photoelectrons, and this is how its value was first calculated in the early twentieth century. In practice, these are no longer the most accurate methods. The CODATA value quoted here is based on three watt-balance measurements of KJ2RK and one inter-laboratory determination of the molar volume of silicon,[1] but is mostly determined by a 2007 watt-balance measurement made at the U.S. National Institute of Standards and Technology (NIST).[15] Five other measurements by three different methods were initially considered, but not included in the final refinement as they were too imprecise to affect the result.
There are both practical and theoretical difficulties in determining h. The practical difficulties can be illustrated by the fact that the two most accurate methods, the watt balance and the X-ray crystal density method, do not appear to agree with one another. The most likely reason is that the measurement uncertainty for one (or both) of the methods has been estimated too low – it is (or they are) not as precise as is currently believed – but for the time being there is no indication which method is at fault.
The theoretical difficulties arise from the fact that all of the methods except the X-ray crystal density method rely on the theoretical basis of the Josephson effect and the quantum Hall effect. If these theories are slightly inaccurate – though there is no evidence at present to suggest they are – the methods would not give accurate values for the Planck constant. More importantly, the values of the Planck constant obtained in this way cannot be used as tests of the theories without falling into a circular argument. Fortunately, there are other statistical ways of testing the theories, and the theories have yet to be refuted.[1]
Josephson constant
The Josephson constant KJ relates the potential difference U generated by the Josephson effect at a "Josephson junction" with the frequency ν of the microwave radiation. The theoretical treatment of Josephson effect suggests very strongly that KJ = 2e/h.
The Josephson constant may be measured by comparing the potential difference generated by an array of Josephson junctions with a potential difference which is known in SI volts. The measurement of the potential difference in SI units is done by allowing an electrostatic force to cancel out a measurable gravitational force. Assuming the validity of the theoretical treatment of the Josephson effect, KJ is related to the Planck constant by
Watt balance
A watt balance is an instrument for comparing two powers, one of which is measured in SI watts and the other of which is measured in conventional electrical units. From the definition of the conventional watt W90, this gives a measure of the product KJ2RK in SI units, where RK is the von Klitzing constant which appears in the quantum Hall effect. If the theoretical treatments of the Josephson effect and the quantum Hall effect are valid, and in particular assuming that RK = h/e2, the measurement of KJ2RK is a direct determination of the Planck constant.
Magnetic resonance
The gyromagnetic ratio γ is the constant of proportionality between the frequency ν of nuclear magnetic resonance (or electron paramagnetic resonance for electrons) and the applied magnetic field B: ν = γB. It is difficult to measure gyromagnetic ratios precisely because of the difficulties in precisely measuring B, but the value for protons in water at 25 °C is known to better than one part per million. The protons are said to be "shielded" from the applied magnetic field by the electrons in the water molecule, the same effect that gives rise to chemical shift in NMR spectroscopy, and this is indicated by a prime on the symbol for the gyromagnetic ratio, γ′p. The gyromagnetic ratio is related to the shielded proton magnetic moment μ′p, the spin number S (S = 1⁄2 for protons) and the reduced Planck constant.
The ratio of the shielded proton magnetic moment μ′p to the electron magnetic moment μe can be measured separately and to high precision, as the imprecisely-known value of the applied magnetic field cancels itself out in taking the ratio. The value of μe in Bohr magnetons is also known: it is half the electron g-factor ge. Hence
A further complication is that the measurement of γ′p involves the measurement of an electric current: this is invariably measured in conventional amperes rather than in SI amperes, so a conversion factor is required. The symbol Γ′p-90 is used for the measured gyromagnetic ratio using conventional electrical units. In addition, there are two methods of measuring the value, a "low-field" method and a "high-field" method, and the conversion factors are different in the two cases. Only the high-field value Γ′p-90(hi) is of interest in determining the Planck constant.
Substitution gives the expression for the Planck constant in terms of Γ′p-90(hi):
Faraday constant
The Faraday constant F is the charge of one mole of electrons, equal to the Avogadro constant NA multiplied by the elementary charge e. It can be determined by careful electrolysis experiments, measuring the amount of silver dissolved from an electrode in a given time and for a given electric current. In practice, it is measured in conventional electrical units, and so given the symbol F90. Substituting the definitions of NA and e, and converting from conventional electrical units to SI units, gives the relation to the Planck constant.
X-ray crystal density
The X-ray crystal density method is primarily a method for determining the Avogadro constant NA but as the Avogadro constant is related to the Planck constant it also determines a value for h. The principle behind the method is to determine NA as the ratio between the volume of the unit cell of a crystal, measured by X-ray crystallography, and the molar volume of the substance. Crystals of silicon are used, as they are available in high quality and purity by the technology developed for the semiconductor industry. The unit cell volume is calculated from the spacing between two crystal planes referred to as d220. The molar volume Vm(Si) requires a knowledge of the density of the crystal and the atomic weight of the silicon used. The Planck constant is given by
Fixation
As mentioned above, the numerical value of the Planck constant depends on the system of units used to describe it. Its value in SI units is known to 50 parts per billion but its value in atomic units is known exactly, because of the way the scale of atomic units is defined. The same is true of conventional electrical units, where the Planck constant (noted h90 to distinguish it from its value in SI units) is given by
with KJ–90 and RK–90 being exactly defined constants. Atomic units and conventional electrical units are very useful in their respective fields, because the uncertainty in the final result doesn't depend on an uncertain conversion factor, only on the uncertainty of the measurement itself.
There are a number of proposals to redefine certain of the SI base units in terms of fundamental physical constants.[22] This has already been done for the metre, which is defined in terms of a fixed value of the speed of light. The most urgent unit on the list for redefinition is the kilogram, whose value has been fixed for all science (since 1889) by the mass of a small cylinder of platinum–iridium alloy kept in vault just outside Paris. While nobody knows if the mass of the International Prototype Kilogram has "changed" since 1889 – the value 1 kg of its mass expressed in kilograms is by definition unchanged and therein lies one of the problems – it is known that over such a timescale the many similar Pt–Ir alloy cylinders kept in national laboratories around the world, have changed their relative mass by several tens of parts per million, however carefully they are stored, and the more so, the more they have been taken out and used as mass standards. A change of several tens of micrograms in one kilogram is equivalent to the current uncertainty in the value of the Planck constant in SI units.
The legal process to change the definition of the kilogram is already underway,[22] but no final decision will be made before the next meeting of the General Conference on Weights and Measures in 2011.[23] The Planck constant is a leading contender to form the basis of the new definition, although not the only one.[23] Possible new definitions include "the mass of a body at rest whose equivalent energy equals the energy of photons whose frequencies sum to 135,639,274×1042 Hz",[24] or simply "the kilogram is defined so that the Planck constant equals 6.62606896×10−34 J·s".
Watt balances already measure mass in terms of the Planck constant: at present, standard mass is taken as "fixed" and the measurement is performed to determine the Planck constant but, were the Planck constant to be fixed in SI units, the same experiment would be a measurement of the mass. The relative uncertainty in the measurement would remain the same.
Mass standards could also be constructed from silicon crystals or by other "atom-counting" methods. Such methods require a knowledge of the Avogadro constant, which fixes the proportionality between atomic mass and macroscopic mass but, with a defined value of the Planck constant, NA would be known to the same level of uncertainty (if not better) than current methods of comparing macroscopic mass.
See also
- Basic concepts of quantum mechanics
- Planck units
- Wave–particle duality
- Stigler's law
Notes
- ↑ 1.0 1.1 1.2 1.3 1.4 Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006". Rev. Mod. Phys. 80: 633–730. doi:10.1103/RevModPhys.80.633. http://physics.nist.gov/cuu/Constants/codata.pdf. Direct link to value.
- ↑ 2.0 2.1 2.2 2.3 2.4 Planck, Max (1901), "Ueber das Gesetz der Energieverteilung im Normalspectrum", Ann. Phys. 309 (3): 553–63, doi:10.1002/andp.19013090310, http://www.physik.uni-augsburg.de/annalen/history/historic-papers/1901_309_553-563.pdf. English translation: "On the Law of Distribution of Energy in the Normal Spectrum".
- ↑ Kragh, Helge (1 December 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com, http://physicsworld.com/cws/article/print/373
- ↑ Kragh, Helge (1999), Quantum Generations: A History of Physics in the Twentieth Century, Princeton University Press, p. 62, ISBN 0691095523, http://books.google.com/?id=ELrFDIldlawC&printsec=frontcover
- ↑ Planck, Max (2 June 1920), The Genesis and Present State of Development of the Quantum Theory (Nobel Lecture), http://nobelprize.org/nobel_prizes/physics/laureates/1918/planck-lecture.html
- ↑ Previous Solvay Conferences on Physics, International Solvay Institutes, http://www.solvayinstitutes.be/Conseils%20Solvay/PreviousPhysics.html, retrieved 12 December 2008
- ↑ 7.0 7.1 7.2 See, eg, Arrhenius, Svante (10 December 1922), Presentation speech of the 1921 Nobel Prize for Physics, http://nobelprize.org/nobel_prizes/physics/laureates/1921/press.html
- ↑ 8.0 8.1 8.2 Lenard, P. (1902), "Ueber die lichtelektrische Wirkung", Ann. Phys. 313 (5): 149–98, doi:10.1002/andp.19023130510
- ↑ Einstein, Albert (1905), "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt", Ann. Phys. 17: 132–48, doi:10.1002/andp.19053220607, http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1905_17_132-148.pdf
- ↑ 10.0 10.1 10.2 10.3 Millikan, R. A. (1916), "A Direct Photoelectric Determination of Planck's h", Phys. Rev. 7: 355–88, doi:10.1103/PhysRev.7.355
- ↑ Bohr, Niels (1913), "On the Constitution of Atoms and Molecules", Phil. Mag., Ser. 6 26: 1–25, doi:10.1080/14786441308634993
- ↑ The main exceptions are the Newtonian constant of gravitation G and the gas constant R. The uncertainty in the value of the gas constant also affects those physical constants which are related to it, such ad the Boltzmann constant and the Loschmidt constant.
- ↑ Kibble, B. P.; Robinson, I. A.; Belliss, J. H. (1990), "A Realization of the SI Watt by the NPL Moving-coil Balance", Metrologia 27 (4): 173–92, doi:10.1088/0026-1394/27/4/002
- ↑ Steiner, R.; Newell, D.; Williams, E. (2005), "Details of the 1998 Watt Balance Experiment Determining the Planck Constant", J. Res. Natl. Inst. Stand. Technol. 110 (1): 1–26, http://nvl.nist.gov/pub/nistpubs/jres/110/1/j110-1ste.pdf
- ↑ 15.0 15.1 Steiner, R. L.; Williams, E. R.; Liu, R.; Newell, D. B. (2007), "Uncertainty Improvements of the NIST Electronic Kilogram", IEEE Trans. Instrum. Meas. 56 (2): 592–96, doi:10.1109/TIM.2007.890590
- ↑ Fujii, K.; Waseda, A.; Kuramoto, N.; Mizushima, S.; Becker, P.; Bettin, H.; Nicolaus, A.; Kuetgens, U.; Valkiers, S.; Taylor, P.; De Bievre, Paul; Mana, G.; Massa, E.; Matyi, R.; Kessler, E.G., Jr.; Hanke, M. (2005), "Present state of the avogadro constant determination from silicon crystals with natural isotopic compositions", IEEE Trans. Instrum. Meas. 54 (2): 854–59, doi:10.1109/TIM.2004.843101
- ↑ Sienknecht, Volkmar; Funck, Torsten (1985), "Determination of the SI Volt at the PTB", IEEE Trans. Instrum. Meas. 34 (2): 195–98, doi:10.1109/TIM.1985.4315300. Sienknecht, V.; Funck, T. (1986), "Realization of the SI Unit Volt by Means of a Voltage Balance", Metrologia 22 (3): 209–12, doi:10.1088/0026-1394/22/3/018. Funck, T.; Sienknecht, V. (1991), "Determination of the volt with the improved PTB voltage balance", IEEE Trans. Instrum. Meas. 40 (2): 158–61, doi:10.1109/TIM.1990.1032905.
- ↑ Clothier, W. K.; Sloggett, G. J.; Bairnsfather, H.; Currey, M. F.; Benjamin, D. J. (1989), "A Determination of the Volt", Metrologia 26 (1): 9–46, doi:10.1088/0026-1394/26/1/003
- ↑ Kibble, B. P.; Hunt, G. J. (1979), "A Measurement of the Gyromagnetic Ratio of the Proton in a Strong Magnetic Field", Metrologia 15 (1): 5–30, doi:10.1088/0026-1394/15/1/002
- ↑ Liu, R.; Liu, H.; Jin, T.; Lu, Z.; Du, X.; Xue, S.; Kong, J.; Yu, B.; Zhou, X.; Liu, T.; Zhang, W. (1995), "A Recent Determination for the SI Values of γ′p and 2e/h at NIM", Acta Metrol. Sin. 16 (3): 161–68
- ↑ Bower, V. E.; Davis, R. S. (1980), "The Electrochemical Equivalent of Pure Silver: A Value of the Faraday Constant", J. Res. Natl. Bur. Stand. 85 (3): 175–91
- ↑ 22.0 22.1 94th Meeting of the International Committee for Weights and Measures (2005). Recommendation 1: Preparative steps towards new definitions of the kilogram, the ampere, the kelvin and the mole in terms of fundamental constants
- ↑ 23.0 23.1 23rd General Conference on Weights and Measures (2007). Resolution 12: On the possible redefinition of certain base units of the International System of Units (SI).
- ↑ Taylor, B. N.; Mohr, P. J. (1999), "On the redefinition of the kilogram", Metrologia 36 (1): 63–64, doi:10.1088/0026-1394/36/1/11, http://www.iop.org/EJ/article/0026-1394/36/1/11/me9111.pdf
References
- Barrow, John D. (2002), The Constants of Nature; From Alpha to Omega - The Numbers that Encode the Deepest Secrets of the Universe, Pantheon Books, ISBN 0-375-42221-8
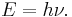
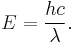
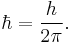
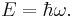
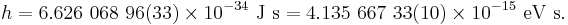

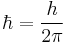
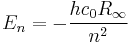
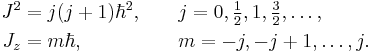
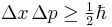
![[\hat{p}_i, \hat{x}_j] = -i \hbar \delta_{ij}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/213762953584068056429b8eb5f43047.png)